Lecture 4: Linear Regression
Presenter Notes

Linear regression, famously used by Gauss in 1809 to predict the location of Ceres, is the ur-model of supervised learning.
Presenter Notes
Problem
Suppose $A \in \mathbb{R}^{m \times n}$ with $m \neq n$ and $y \in \mathbb{R}^m$ is a given vector. Find $x \in \mathbb{R}^n$ such that $y = Ax$. $$ $$ However if no $x$ satisfies the equation or more than one $x$ does -- that is the solution is not unique -- the problem is said not to be well posed.
Presenter Notes
The standard approach in the (overdetermined) case where $m > n$ is linear least squares linear regression. $$ $$ In this situation the linear system $Ax = y$ is not solvable for most values of $y$. $$ $$ The linear least squares problem poses an approximate solution in the following constrained optimization problem:
$$ \min_{b \in \mathcal{Im}(A)} \|y - b\|^2 $$
Presenter Notes
Pseudoinverses
The SVD gives us a nice way of studying linear systems $Ax = y$ where the matrix is not invertible. $$ $$ In this case $A$ has a generalized inverse called the Moore-Penrose psuedoinverse (denoted $A^+$). $$ $$ The Moore-Penrose psuedoinverse is defined for any real-valued matrix $A$, and corresponds to the normal inverse $A^{-1}$ when $A$ is invertible.
Presenter Notes
We write $\oplus$ for the direct sum of inner product spaces, $\perp$ for the orthogonal complement, $\mathcal{Ker}$ for the kernel of a map, and $\mathcal{Im}$ for the image of a map. $$ $$ If we view the matrix as a linear map $A :\mathcal{X} \to \mathcal{Y}$ then $A$ decomposes the two spaces as follows:
\begin{align} \mathcal{X} &= \mathcal{Ker}(A )^\perp \oplus\mathcal{Ker}(A ) \newline \mathcal{Y} &= \mathcal{Im}(A )^\perp \oplus\mathcal{Im}(A ) \end{align}
Presenter Notes
The restriction $A : \mathcal{Ker}(A )^\perp \to \mathcal{Im}(A)$ is then an isomorphism. $$ $$ $A^+$ is defined on $ \mathcal{Im}(A)$ to be the inverse of this isomorphism, and on $ \mathcal{Im}(A)^\perp$ to be zero. $$ $$ Therefore for $y \in \mathcal{Im}(A)$, $A^+y$ is the unique vector $x$ such that $y = A(x)$ and $x \in \mathcal{Ker}(A)^\perp$.
Presenter Notes
This construction gives us the following nice properties for $A^+$:
\begin{align}
\mathcal{Ker}(A^+) &= \mathcal{Im}(A)^\perp
\newline
\mathcal{Im}(A^+) & = \mathcal{Ker}(A)^\perp
\end{align}
Presenter Notes
Exercise
What is the pseudoinverse of $X$?
$$ X = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ \end{pmatrix} $$
Presenter Notes
Properties
- If $A$ has real entries, then so does $ A^+$.
- If $A$ is invertible, its pseudoinverse is its inverse. That is: $A^+=A^{-1}$.
- The pseudoinverse of the pseudoinverse is the original matrix: $(A^+)^+=A$.
- Pseudoinversion commutes with transposition:$(A^T)^+ = (A^+)^T$.
- The pseudoinverse of a scalar multiple of $A$ is the reciprocal multiple of $A$: $(\alpha A)^+ = \alpha^{-1} A^+$ for $\alpha\neq 0$.
Presenter Notes
Theorem (Analytic Characterization): Let $A \in \mathbb{R}^{n \times m}$. Then
$$
A^+ = \lim_{\lambda \to 0} (A^TA + \lambda I)^{-1} A^T
$$
This characterization (known as Tikhonov regularization) leads to an iterative method for computing $A^+$ (see Ben-Israel and Cohen).
note the connection to ridge regression.
Presenter Notes
Exercise
Find the pseudoinverse of $A$ by checking the conditions of the above theorem.
$$ A = \begin{pmatrix} 1 & 1 \\ 1 & 1 \\ \end{pmatrix} $$
Presenter Notes
Presenter Notes
\begin{split}
A^+ &= \lim_{\lambda \to 0} (A^TA + \lambda I)^{-1} A^T
\newline
&= \lim_{\lambda \to 0}
\begin{pmatrix}
2+\lambda & 2 \\
2 & 2+\lambda \\
\end{pmatrix} ^ {-1}
\begin{pmatrix}
1 & 1 \\
1 & 1 \\
\end{pmatrix}
\newline
&= \lim_{\lambda \to 0} \frac{1}{\lambda(\lambda+4)}
\begin{pmatrix}
2+ \lambda & -2 \\
-2 & 2 + \lambda \\
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 1 \\
\end{pmatrix}
\newline
&= \lim_{\lambda \to 0} \frac{1}{\lambda(\lambda+4)}
\begin{pmatrix}
\lambda & \lambda \\
\lambda & \lambda \\
\end{pmatrix}
\newline
&= \lim_{\lambda \to 0} \frac{1}{\lambda+4}
\begin{pmatrix}
1& 1 \\
1 & 1\\
\end{pmatrix}
\newline
&= \frac{1}{4}
\begin{pmatrix}
1 & 1 \\
1 & 1\\
\end{pmatrix}
\end{split}
Presenter Notes
We can also define $A^+$ for all $A \in \mathbb{R}^{n \times m}$ according to purely algebraic criteria. $$ $$ Theorem (Algebraic Characterization): Let $A \in \mathbb{R}^{m \times n}$. Then $G = A^+$ if and only if:
- $A G A = A $
- $G A G = G $
- $(A G)^T = AG $
- $(G A)^T = GA $
Furthermore, $ A^+$ always exists and is unique. Note also that when an true $A^{-1}$ exists it satisfies the above properties.
Presenter Notes
A conceptually simpler way to compute the pseudoinverse is by using the SVD of $A$. $$ $$ If $A = U\Sigma V^T$ is the singular value decomposition of $A$ then $A^+ = V\Sigma^+ U^T$. $$ $$ For a rectangular diagonal matrix such as $\Sigma$, we can easily get the pseudoinverse by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and then transposing the matrix, as in the Exercise above.
In numerical computation, only elements larger than some small tolerance are taken to be nonzero, and the others are replaced by zeros.
Presenter Notes
Example
Lets compute psuedoinverse using the SVD of the matrix $X$ from the last lecture.
$$ X = \begin{pmatrix} 1 & 2 \\ 2 & 1 \\ 3 & 4 \\ 4 & 3 \\ \end{pmatrix} $$
Presenter Notes
We saw that the SVD of $X$ is: $$ \begin{pmatrix} 1 & 2 \\ 2 & 1 \\ 3 & 4 \\ 4 & 3 \\ \end{pmatrix} = \begin{pmatrix} \frac{3}{\sqrt{116}} & \frac{1}{2} \\ \frac{3}{\sqrt{116}} & -\frac{1}{2} \\ \frac{7}{\sqrt{116}} & \frac{1}{2} \\ \frac{7}{\sqrt{116}} & -\frac{1}{2} \\ \end{pmatrix} \begin{pmatrix} \sqrt{58} & 0 \\ 0 & \sqrt{2} \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \end{pmatrix} $$
Presenter Notes
Therefore the pseudoinverse $X^+$ is:
\begin{split} X^+ &= \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{58}} & 0 \\ 0 & \frac{1}{\sqrt{2}} \\ \end{pmatrix} \begin{pmatrix} \frac{3}{\sqrt{116}} & \frac{3}{\sqrt{116}} & \frac{7}{\sqrt{116}} & \frac{7}{\sqrt{116}} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \end{pmatrix} \newline &= \frac{1}{58} \begin{pmatrix} -13 & 16 & -11 & 18 \\ 16 & -13 & 18 & -11 \\ \end{pmatrix} \end{split}
Presenter Notes
Note that both the SVD and the Moore-Penrose psuedoinverse have poor sparsity properties. $$ $$ As such, these methods have limited utility for very large matrices.
Presenter Notes
The following special case will be useful in solving the linear least squares problem. $$ $$ Proposition: If $A$ is injective (e.g. $A$ is full rank and $m \geq n$), then $A^+ = (A^TA)^{-1} A^T $ $$ $$ The proof follows from the algebraic criteria above and the fact that $A^TA$ is a positive definite matrix.
Presenter Notes
Example
For any (column) vector $x \neq 0$:
$$ x^+ = (x^Tx)^+x^T = (x^Tx)^{-1}x^T $$
Presenter Notes
In the linear least squares context, the system: $$ \beta = A^+y = (A^TA)^{-1} A^T y $$ i.e. the Moore-Penrose psuedoinverse of $A$ applied to $y$, is referred to as the normal equations. $$ $$ The matrix $(A^TA)^{-1} A^T$ itself is sometimes referred to as the 'hat matrix'.
Presenter Notes
Exercise
Given the following data: $(1,2), (2,1), (3,4), (4,3)$, treat the second variable as the dependent feature $y$ and compute the linear least squares solution $\beta = A^+y $.
beta = 28/30, whereas PCA would give 1. explain the difference between the two.
Presenter Notes
Exercise
Given the following data: $(1,2,4), (2,1,3), (3,4,2), (4,3,1)$, treat the third variable as the dependent feature $y$ and compute the linear least squares solution $\beta = A^+y $.
Presenter Notes
Presenter Notes
We use the pseudoinverse matrix we computed above: \begin{split} \beta &= A^+y \newline &= \frac{1}{58} \begin{pmatrix} -13 & 16 & -11 & 18 \\ 16 & -13 & 18 & -11 \\ \end{pmatrix} \begin{pmatrix} 4 \\ 3 \\ 2 \\ 1 \\ \end{pmatrix} \newline &= \frac{1}{58} \begin{pmatrix} -8 \\ 50 \\ \end{pmatrix} \end{split}
Presenter Notes
$A^+y$ is the orthogonal projection of $y$ onto the m-dimensional subspace spanned by $\mathcal{Im}(A)$. $$ $$ This implies that the error $ y - A\beta = y - AA^+y $ is in the kernel of $A^T$, i.e. $A^T(y -A\beta) = 0$. $$ $$
Presenter Notes
Exercise
Show that for the regression problem above, $ y - A\beta$ is in the kernel of $A^T$.
Presenter Notes
Probability Model
Linear regression is a discriminative regression model of the form:
$$ p(y| x, \beta) = \mathcal{N}( \beta^T x, \sigma^2) $$ where $\beta$ is an unknown vector and $x, \beta \in \mathbb{R}^n$. $$ $$ Note that the model can easily be extended to non-linear relationships by transforming the vector $x$ beforehand. It is still linear in $\beta$ and still referred to as linear regression.
Presenter Notes
We fit the unknown coefficient vector $\beta \in \mathbb{R}^m $ by maximizing a log liklifood function. This is a common pattern in machine learning that we will see several times.
\begin{split} L(\beta) & = \sum_{i=1}^N \log (p(y_i| x_i, \beta)) \newline & = \sum_{i=1}^N \log \left( \frac{1}{\sqrt{2 \pi} \sigma} exp(-\frac{1}{2 \sigma^2}(y_i - \beta^T x_i)^2 ) \right) \newline & = -\frac{N}{2} \log(2 \pi \sigma^2) -\frac{1}{2 \sigma^2} \sum_{i=1}^N (y_i - \beta^T x_i)^2 \end{split}
Presenter Notes
This is equivalent to minimizing the following quantity, known as the residual sum of squares (RSS):
$$ \frac{1}{2} \sum_{i=1}^N (y_i - \beta^T x_i)^2 = \frac{1}{2} \sum_{i=1}^N \epsilon_i^2 = \frac{1}{2} \|\epsilon\|^2 $$
The model generally assumes that the 'errors' are i.i.d. (independant and identically distributed).
Presenter Notes
This is not necessarily an accurate assumption, as the following counter-examples (known as Anscombe's quartet) show:
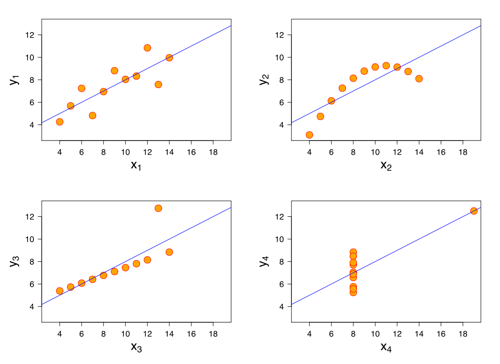
Presenter Notes
Rewriting the RSS in vector form we get:
$$ \frac{1}{2} (y - X\beta)^T (y - X\beta) = \frac{1}{2} \beta^T (X^TX) \beta - \beta^T(X^Ty) $$
Taking the derivative wrt $\beta$ and setting to zero we again get the normal equations:
\begin{split}
X^TX \beta &= X^T y
\newline
\beta &= (X^TX)^{-1} X^T y
\end{split}
If the data vectors $x_i$ are linearly independant then the matrix $X^TX$ will be positive definite and therefore invertible. However in general we will use optimization methods such as Newton-Raphson for calculating $\beta$.
Presenter Notes
Ridge Regression
Returning to our problem statement $y = Ax$, most real-world phenomena have the effect of low-pass filters in the forward direction. $$ $$ Therefore in solving the inverse-problem, $A^+$ operates as a high-pass filter with the undesirable tendency of amplifying noise: the largest singular values in the reverse mapping were the smallest in the forward mapping. $$ $$ In addition, ordinary least squares implicitly nullifies every element of the reconstructed version of $x$, $\beta$ that is in the kernel of $A$, rather than allowing for a model to be used as a prior for $\beta$.
Presenter Notes
Tikhonov regularization (aka ridge regression) adds to the linear least squares model a second constraint that $\|\beta\|^2$ cannot greater than a given value:
$$
\min_{\beta \in \mathcal{Im}(X),\|\beta\|^2 \leq c } \|y - \beta\|^2
$$
Equivalently, we may solve an unconstrained minimization of the least-squares penalty with $\lambda\|\beta\|^2$ added, where $\lambda$ is a constant (this is the Lagrange multipliers form of the constrained problem):
$$
\min_{\beta} \|y - X\beta\|^2 + \lambda\|\beta\|^2
$$
Presenter Notes
In a Bayesian context, this is equivalent to placing a zero-mean normally distributed prior distribution on the parameter vector $\beta$:
$$
p(\beta) = \mathcal{N}(0,\tau^2)
$$
where $\frac{1}{\tau^2}$ controls the strength of the prior.
Our probability model then becomes:
$$ p(y, \beta | x) = p(y | x, \beta) p(\beta) = \mathcal{N}( \beta^T x, \sigma^2) * \mathcal{N}(0,\tau^2) $$
Presenter Notes
The corresponding MAP estimation problem is equivalent to the Lagrange multipliers form of the constrained optimization problem above:
\begin{split}
L(\beta) & = \sum_{i=1}^N \log (p(y_i| x_i, \beta)p(\beta) )
\newline
& = -\frac{N}{2} \log(2 \pi \sigma^2) -\frac{1}{2 \sigma^2} \sum_{i=1}^N (y_i - \beta^T x_i)^2 -\frac{1}{2} \log(2 \pi \tau^2) -\frac{1}{2 \tau^2} \sum_{i=2}^n (\beta_i)^2
\newline
& \propto \|y - X\beta\|^2 + \lambda \|\beta\|^2
\end{split}
where the parameter $\lambda = \frac{\sigma^2}{\tau^2}$.
Note that the second sum generally starts at $i=2$ due to the presence of an unpenalized offset term.
Presenter Notes
The solution is a regularized version of the normal equations (hence the name Tikhonov regularization): $$ \beta = (X^TX + \lambda I)^{-1} X^T y $$ where $I$ is the $n \times n$ identity matrix. $$ $$ These equations are preferable to solve numerically, especially if $X$ is poorly conditioned or rank-deficient (as is the case when several of the features are highly correllated). Note also the connection with the Tikhonov regularization form of the psuedoinverse.
Presenter Notes
Using the SVD of $X$, we have that:
\begin{split}
X\beta &= X(X^TX + \lambda I)^{-1} X^T y
\newline
&= U\Sigma V^T (V\Sigma^2V^T + \lambda I)^{-1} V\Sigma U^T y
\newline
&= U \Sigma (\Sigma^2 + \lambda I)^{-1} \Sigma U^T y
\newline
&= \sum_{i=1}^n \frac{\sigma_i^2}{\sigma_i^2 + \lambda}u_i u_i^T y
\end{split}
Like linear regression, ridge regression expresses $y$ in terms $U$.
It then shrinks these coordinates by the factors $ \frac{\sigma_i^2}{\sigma_i^2 + \lambda}$, penalizing the basis vectors associated with smaller singular values.