Lecture 10a: Algebird in Spark

Presenter Notes

Algebird

"Abstract algebra for Scala. This code is targeted at building aggregation systems (via Scalding or Storm)."

Algebraic structures like semigroup and monoid, as Scala traits
Many useful monoids, to fit common aggregation patterns
However, dependent in production on:
- Spark
- Scalding (batch jobs)
- Storm (streaming)
- or Summingbird ( batch or real time )

Presenter Notes

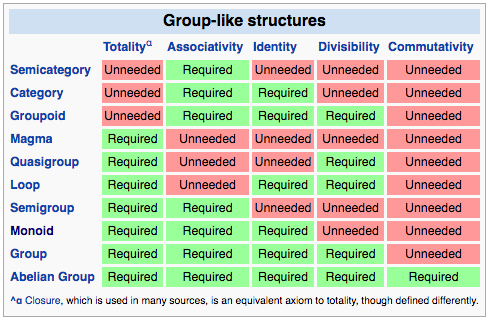
Monoid review

"In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with

(1) a single associative binary operation

and

(2) an identity element."

Commutativity of the binary operation is useful, but not required.

https://en.wikipedia.org/wiki/Monoid

Presenter Notes

Associativity allows some parallelism.

We want aggregation a + b + c + d

a + b + c + d == 
a + (b + (c + d)) ==
(a + b) + (c + d)

This "splitting" pattern of parallelism is exemplified by exercise 10.7: foldMapV

Later, commutativity

Presenter Notes

Count-Min Sketch

"the Sketch ... uses summary based techniques for delivering approximation queries, gets around the typical problems that sampling techniques have and are highly parallelizable in practice."

Count-Min Sketch - A Data Structure for Stream Mining Applications

Wiki

Presenter Notes

Count-Min Sketches can be combined

class CMS[K] { 
  ...
  // Returns a new sketch that is the combination 
  // of this sketch and the other sketch.
  def ++(other: CMS[K]): CMS[K]
  ...
}

CMS

Presenter Notes

Count-min Sketch Monoid

class CMSMonoid[K] extends Monoid[CMS[K]]

Count-Min Sketches under combination form a Monoid. The identity element is an empty sketch. It has a generic for the type being counted.

val cmsMonoid: CMSMonoid[Int] = {
  val eps = 0.001
  val delta = 1E-10
  val seed = 1
  CMS.monoid[Int](eps, delta, seed)
}

Presenter Notes

// def create(item: K): CMS[K] 
// Creates a sketch out of a single item.
val sketch1: CMS[Int] = cmsMonoid.create(4)
val sketch2: CMS[Int] = cmsMonoid.create(4)
val sketch3: CMS[Int] = cmsMonoid.create(6)

val aggregatedSketch: CMS[Int] = 
  sketch1 ++ sketch2 ++ sketch3

in slideCode.lecture10a.CountMinSketchUsage and slideCode.lecture10a.SketchExample

Presenter Notes

frequency of 4 in sketch1 = 
  Approximate(1,1,1,1.0)
frequency of 6 in sketch1 = 
  Approximate(0,0,0,1.0)

frequency of 4 in aggregatedSketch = 
  Approximate(2,2,2,0.9999999999)
frequency of 6 in aggregatedSketch = 
  Approximate(1,1,1,0.9999999999)

in slideCode.lecture10a.SketchExample

Presenter Notes

Algebird example

Counting approximate number of Tweets per user;

an example of a Key-Value aggregation

case class Tweet(userId: Int, message: String, 
                 time: DateTime)

def generateTweets(n: Int): Seq[Tweet] = ...

in slideCode.lecture10a.Tweets

Presenter Notes

val tweets: Seq[Tweet] = generateTweets(32)

val userIds: Seq[Int] = 
  tweets.map { tweet => tweet.userId }

// cmsMonoid.create(data: Seq[K]): CMS[K]`
// Creates a sketch out of multiple items.
val sketch: CMS[Int] = cmsMonoid.create(userIds)

This version of create folds with the Monoid. It hides a lot under the hood.

It useful for one-off experimentation, but not production use of the CMSMonoid.

in slideCode.lecture10a.CountMinSketchUsage and slideCode.lecture10a.CountMinSketchUsageExample

Presenter Notes

Values in the Sketch

Count Min Sketch counts
user 0 Approximate(1,1,1,0.9999999999)
user 1 Approximate(3,3,3,0.9999999999)
user 2 Approximate(1,1,1,0.9999999999)
user 3 Approximate(2,2,2,0.9999999999)
user 4 Approximate(0,0,0,1.0)
user 5 Approximate(1,1,1,0.9999999999)
...

Presenter Notes

exact counts
user 0 exact count Some(1)
user 1 exact count Some(3)
user 2 exact count Some(1)
user 3 exact count Some(2)
user 4 exact count None
user 5 exact count Some(1)

Presenter Notes

Commutativity improves parallelism further and reduces storage requirements.

Reducing storage requirements is the essence of "real-time" streaming analysis.

We want aggregation a + b + c + d

Imagine a stream where c and d arrive first, b second and a third.

c + d = e

(e + b) + a ==
c + d + b + a

Sources at 7:40 and 12:45

Presenter Notes

Source: Outline of algebraic structures

Presenter Notes

There is no data type in Algebird that connotates commutativity. Discussion

There is only run-time checking

def isCommutativeEq[T: Semigroup]
  (eqfn: (T, T) => Boolean) = 
  'isCommutativeEq |: forAll { (a: T, b: T) =>
    val semi = implicitly[Semigroup[T]]
    eqfn(semi.plus(a, b), semi.plus(b, a))
  }

Some of this method should look familiar from our monoid laws exercise in lab 10

in package com.twitter.algebird.BaseProperties

Presenter Notes

Max Monoid in Spark

Calculate (exact) maximum score of any game in basketball_scores.csv

read CSV

val df: DataFrame = ...

CSV

...,TeamName,...,ScoreOff,...
...,Abilene Christian,...,57,...
...,Abilene Christian,...,100,...
...,Abilene Christian,...,72,...
...
...,Alabama St.,...,73,...
...

Presenter Notes

Wrap each score in a Max object

val maxScores: RDD[Max[Int]] = 
  df.map { (r: Row) => Max(r.getInt(5)) }
//        5th column; 0-indexed     ^

Reduce the Max objects to a single Max object

val maxScore: Max[Int] = 
  maxScores.reduce { (m1, m2) => m1.+(m2) }

in spark.lecture10a.MaxScoreExample

Presenter Notes

(m1, m2) => m1.+(m2)

Infix notation for Max is buried in Algebird library. There is not a clear connection between infix + and the Max class. Contrast this with HyperLogLog, later.

Presenter Notes

Pair RDD

Calculate max score by team

Want to apply this method:

def reduceByKey(func: (V, V) ⇒ V): RDD[(K, V)]

Key by team name

val keyedScores: RDD[(String, Max[Int])] = 
  keyedRDD.map { (tup: (String, Row)) => {
    val teamName = tup._1
    val row = tup._2
    val score = row.getInt(5)
    (teamName, Max(score))
  }
}

in spark.lecture10a.MaxScoreExample

Presenter Notes

val maxScoreByTeam: RDD[(String, Max[Int])] = 
  keyedScores.reduceByKey { (s1, s2) => s1+s2 }

maxScoreByTeam.foreach { 
  case (teamName: String, maxScore: Max[Int]) => 
  println(s"Team $teamName  max score $maxScore")}

Presenter Notes

Output

Team Massachusetts  max score Max(108)
Team Hampton  max score Max(98)
Team Winthrop  max score Max(102)
Team Alabama St.  max score Max(86)
...

Presenter Notes

Count-min sketch in Spark

Estimate the number of games each team has played

val df: DataFrame = ...

val cmsMonoid: CMSMonoid[String] = {
  val eps = 0.001
  val delta = 1E-10
  val seed = 1
  CMS.monoid[String](eps, delta, seed)
}

in spark.lecture10a.CountMinSketchExample

Presenter Notes

Create sketch of team name of each row

val teamSketches: RDD[CMS[String]] = 
  df.map { (row: Row) => 
    cmsMonoid.create(row.getString(1)) }

Reduce sketches to single sketch

val counts: CMS[String] = 
  teamSketches.reduce { (s1, s2) => 
    cmsMonoid.plus(s1, s2) }

Presenter Notes

Find distinct team names

val teams: RDD[String] = 
  df.map { (row: Row) => 
    row.getString(1) }.distinct()

Extract frequency of each key in aggregate sketch

teams.foreach { teamName =>
  val freqEstimate = 
    counts.frequency(teamName).estimate
  println(s"... $teamName ... $freqEstimate ...")
}

Presenter Notes

Team Tennessee Tech played an estimated 28 games
Team Western Mich. played an estimated 30 games
Team Savannah St. played an estimated 29 games
Team Campbell played an estimated 27 games
Team Memphis played an estimated 34 games
Team Colorado St. played an estimated 32 games
Team Bowling Green played an estimated 32 games
Team Loyola Maryland played an estimated 30 games
Team Hampton played an estimated 30 games
Team Massachusetts played an estimated 32 games
Team Winthrop played an estimated 29 games
...

Presenter Notes

HyperLogLog in Spark

Estimate the number of unique rows

val df: DataFrame = ...

val hll = new HyperLogLogMonoid(12)

Presenter Notes

Hash and sketch each Row

r.hashCode incorporates every value in the row.

val rowHashes: RDD[HLL] = 
  df.map { (r: Row) => hll(r.hashCode) }

Combine sketches into single sketch

val uniqueRowCount: HLL = 
  rowHashes.reduce( (hll1, hll2) => 
    hll.plus(hll1, hll2) )

Presenter Notes

println("..."+
         uniqueRowCount.estimatedSize.toLong)

Output

estimated unique rows in data frame: 10813

Presenter Notes

If two rows are identical, they will produce the same hash code.

row 1: [a,b,123]
row 2: [a,b,123]
row 1 hash code: 345508721
row 2 hash code: 345508721

in spark.lecture10a.IdenticalRows

Presenter Notes

Estimate number of unique teams, taken from TeamName column

Hash and make sketch of each team name

val teamSketches: RDD[HLL] = 
  df.map { (r: Row) =>
    hll(r(1).hashCode) }
//        ^ TeamName column

Presenter Notes

Reduce sketches to single sketch

val uniqueTeams: HLL =
  teamSketches.reduce( (hll1, hll2) => 
    hll.plus(hll1, hll2) )

println("..."+
        uniqueTeams.estimatedSize.toLong)

Output

estimate of number of unique teams: 358

Presenter Notes

Product monoid

Calculate max score and estimate games played by team, in one sweep through the data

Use Max and HLL

val df: DataFrame = ...

val hll = new HyperLogLogMonoid(12)

key by team name

val keyedRDD: RDD[(String, Row)] = 
  df.rdd.keyBy { (r: Row) => r.getString(1) }

in spark.lecture10a.MaxScoreAndGamesPlayed

Presenter Notes

Our product monoid

val productMonoid: Monoid[(Max[Int], HLL)] =
  new Product2Monoid(
    (mi: Max[Int], h: HLL) => (mi, h),
    (t: (Max[Int],HLL)) => Some(t))
    (Max.intMonoid, hll)

in spark.lecture10a.MaxScoreAndGamesPlayed

Presenter Notes

val scoresAndCounts:RDD[(String,(Max[Int], HLL))]= 
  keyedRDD.map{ case (teamName: String,row: Row)=>
    val score = row.getInt(5)
    val maxScore: Max[Int] = Max(score)
    val rowSketch: HLL = hll(row.hashCode())
    (teamName, (maxScore, rowSketch))
  }

Presenter Notes

Reduce the products (Max[Int], HLL) into a single product, per key

val scoreAndCount:RDD[(String,(Max[Int],HLL))] =
  scoresAndCounts.reduceByKey { 
    (tup1:(Max[Int],HLL), tup2:(Max[Int],HLL)) =>
    productMonoid.plus(tup1, tup2)
  }

Presenter Notes

scoreAndCount.foreach { 
  case (teamName: String, tup: (Max[Int], HLL)) => 
  println(s"Team $teamName  ... ${tup._1} ...
            ... ${tup._2.estimatedSize.toLong}")}

Output

Team Tennessee Tech  max score Max(101) 
                     games played 28
Team Western Mich.  max score Max(94) 
                     games played 30
Team Campbell  max score Max(101) 
                games played 27
Team Savannah St.  max score Max(76) 
                    games played 29
...